如何计算矩阵乘法时间复杂度

引言

最近在看Swin Transformer论文的时候被其中的矩阵计算时间复杂度卡住了

趁机学习一下如何计算矩阵乘法的时间复杂度

矩阵乘法时间复杂度计算方法

知乎上有这样一个问题

三个矩阵相乘的复杂度是多少？

比方说矩阵A是mxn,B是nxm,C是mxn，我知道$A*B$的复杂度是$m^2*n$ ,那$A*B*C$复杂度是多少呢

首先考虑两个矩阵相乘的时间复杂度，假设A是一个$m*n$的矩阵，B是一个$n*l$的矩阵

矩阵相乘的每一次计算可以分为如下三个步骤：

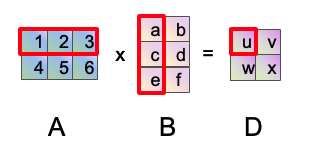
1. 首先我们取A矩阵的一行
2. 我们取B矩阵的一列
3. 然后把每一个对应位置的元素进行相乘相加，也就是$u=1*a+2*c+3*e$

用代码实现的话如下所示，假设A是一个2x3的矩阵，可以简单理解为二维数组，B是3x2的矩阵，计算结果D是2x2的矩阵

sum = 0
count = 0
for iA_row in range(A.row): # 遍历矩阵A的行 
  for iB_col in range(B.col): # 遍历矩阵B的列 
    for i_sum in range(A.col): # 循环把每个元素相加
      sum += A[iA_row][i_sum] * B[iB_col][i_sum] # 执行元素相加操作
      D[count%D.row][count/D.row] = sum # 把计算结果放在矩阵D中
      count += 1
      sum = 0

这样看的话，时间复杂度就是$O(mln)$，因为第一个循环会执行矩阵A的行数次，也就是$m$次，第二个循环会执行矩阵B的列数次，也就是$l$次，第三个矩阵会执行A的列数B的行数次，也就是$n$次，所以三个循环叠加的总时间复杂度是$O(mln)$

按照题中A是$m*n$，B是$n*m$的矩阵，则时间复杂度是$O(m^2n)$次

那么三个矩阵相乘的时间复杂度是多少呢

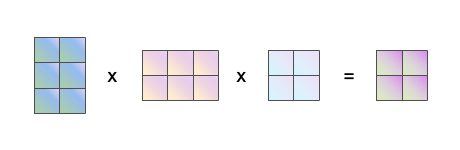
三个矩阵相乘，根据乘法结合律，可以分解为两次两个矩阵相乘

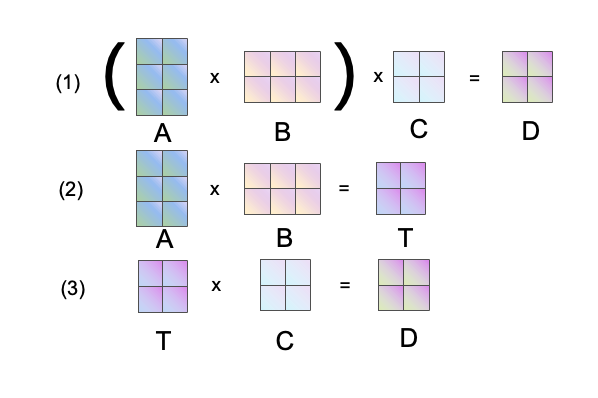
而在代码实现中，我们也是先算前两个矩阵的乘法，再算前两个矩阵的乘积和第三个矩阵的乘法，为了方便说明给这几个矩阵标上名字

代码实现如下，假设A是一个$m*n$的矩阵，B是一个$n*l$的矩阵，C是一个$l*p$的矩阵

# 前两个矩阵乘法的代码和上面相同
sum = 0
count = 0
for iA_row in range(A.row): # 遍历矩阵A的行 
  for iB_col in range(B.col): # 遍历矩阵B的列 
    for i_sum in range(A.col): # 循环把每个元素相加
      sum += A[iA_row][i_sum] * B[iB_col][i_sum] # 执行元素相加操作
      T[count%T.row][count/T.row] = sum # 把计算结果放在矩阵D中
      count += 1
      sum = 0    
# 再乘第三个矩阵
count = 0
for iT_row in range(T.row):
  for iC_col in range(C.col):
    for i_sum in range(T.col):
      D[count%D.row][count/D.row] = sum
      count += 1
      sum = 0

这里我们可以发现，这两个矩阵是分别执行的，而在计算时间复杂度时，是忽略常数项的，换句话说，一段代码的时间复杂度是这段代码中最耗时的一个循环的时间复杂度，什么意思呢

就是说以上这段代码的第一个三重循环时间复杂度是$O(mln)$，第二个三重循环的时间复杂度是$O(mlp)$

则这段代码的时间复杂度是$max(O(mln), O(mlp))$

回到最上面知乎那个问题，可知问题中$A*B*C$的时间复杂度是$max(O(m^2n),O(m^2n))=O(m^2n)$

Swin-Transformer中的时间复杂度计算

待续