吴恩达机器学习课程
Week One
什么是机器学习?
Arthur Samuel将机器学习定义为:”使计算机无需明确编程就可以学习的研究领域。“
Tom Mitchell将机器学习定义为:”如果计算机程序在任务T上的性能P随着经验E而提高,则称计算机程序从经验E中学习某类任务T和性能度量P。“
通常情况下,机器学习可以分为监督学习和非监督学习。
监督学习
例子:房价预测,给定一些关于房子的信息和它所对应的房价,通过机器学习方法预测更多的房子售价。也就是说在数据集中包含任务的正确答案。
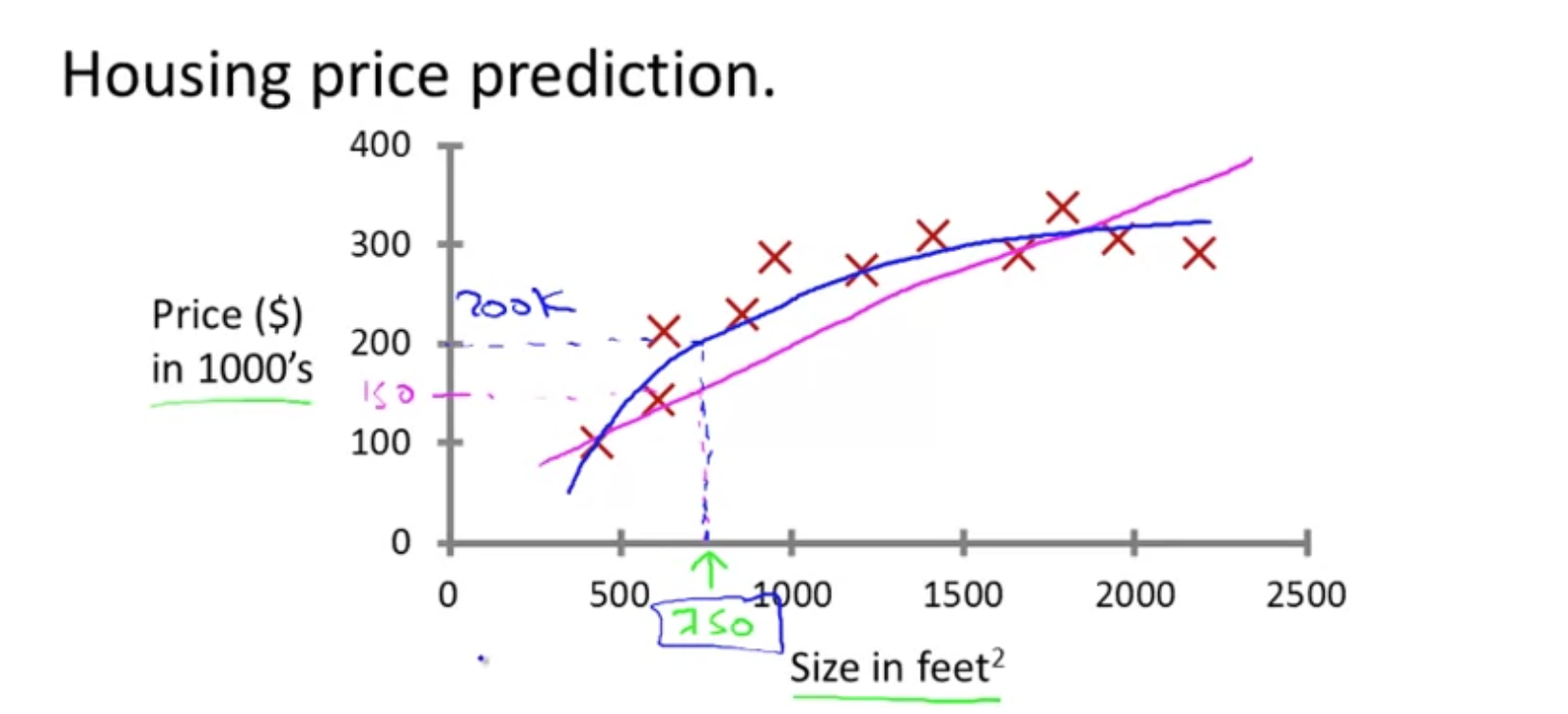
这种任务也被称为回归任务,回归任务的意思是我们试图预测一个连续的输出值。
另一类任务被称为分类任务,分类任务试图预测离散值,例如肿瘤检测任务,对每一个肿瘤的数据(图像或其他描述数据)进行预测,预测出这个肿瘤是良性还是恶性。
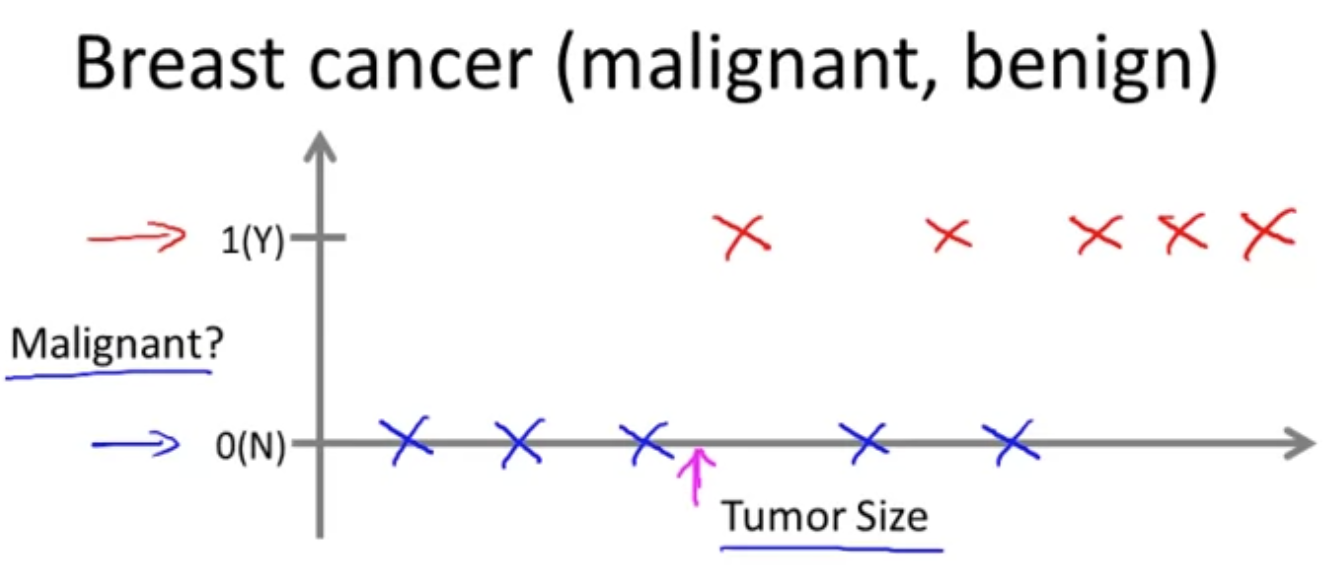
分类任务可能是二分类或者更多种类的分类,上图中是一个二分类的任务。并且在上图所示的任务中对于每个肿瘤只有一种特征(Tumor Size),在应用中,每一条数据往往有更多特征进行描述。
非监督学习
在监督学习中,每一条数据都有他对应的标签,如图所示对于每个点都标记为⭕️或者❎。
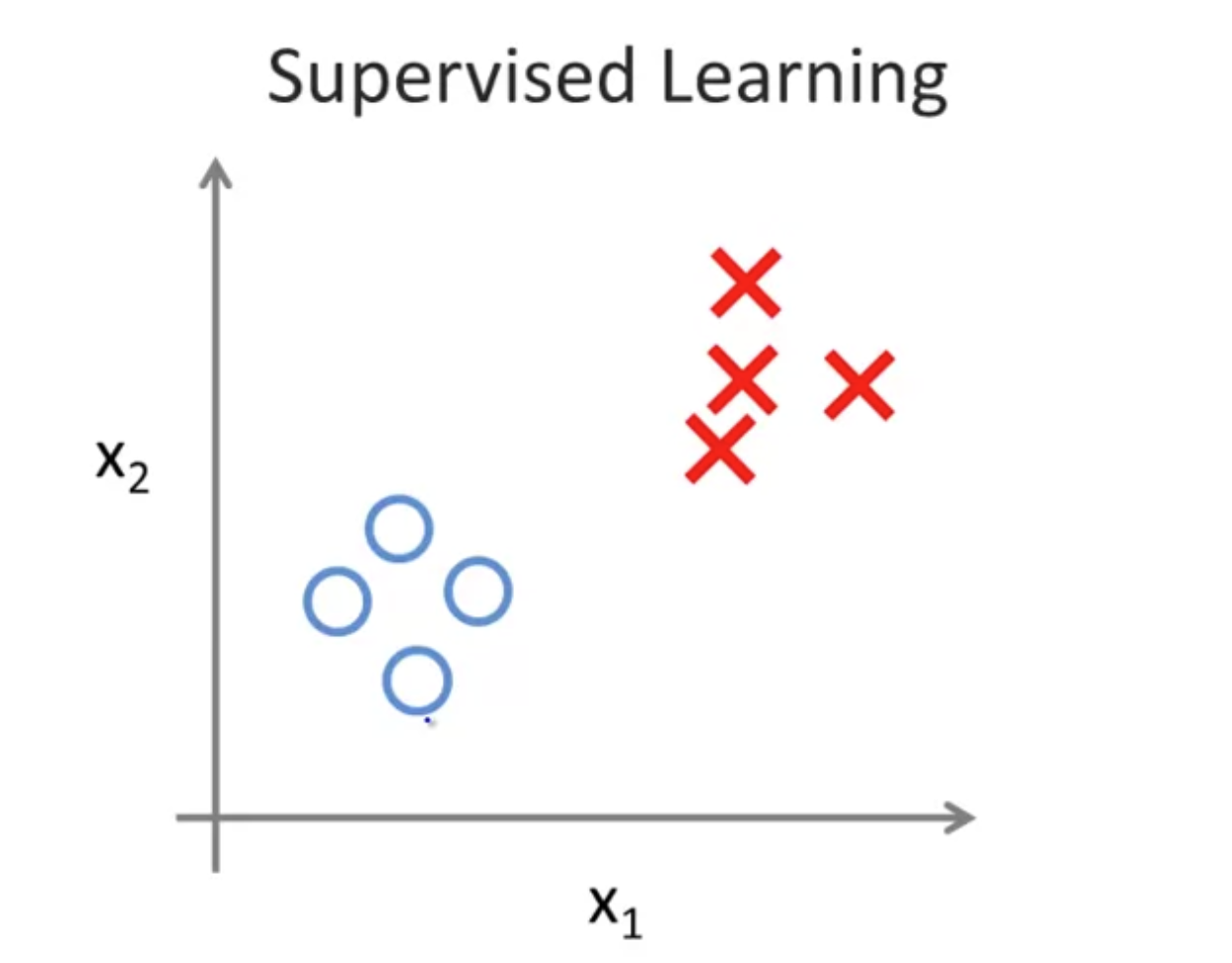
而在非监督学习中,数据并没有明确的标签,所有数据看起来都是相同的,但是直观看起来,这些数据可以被分为两堆,这样每一个堆称为一个簇。将非监督的数据分成簇的方法被称为聚类算法。
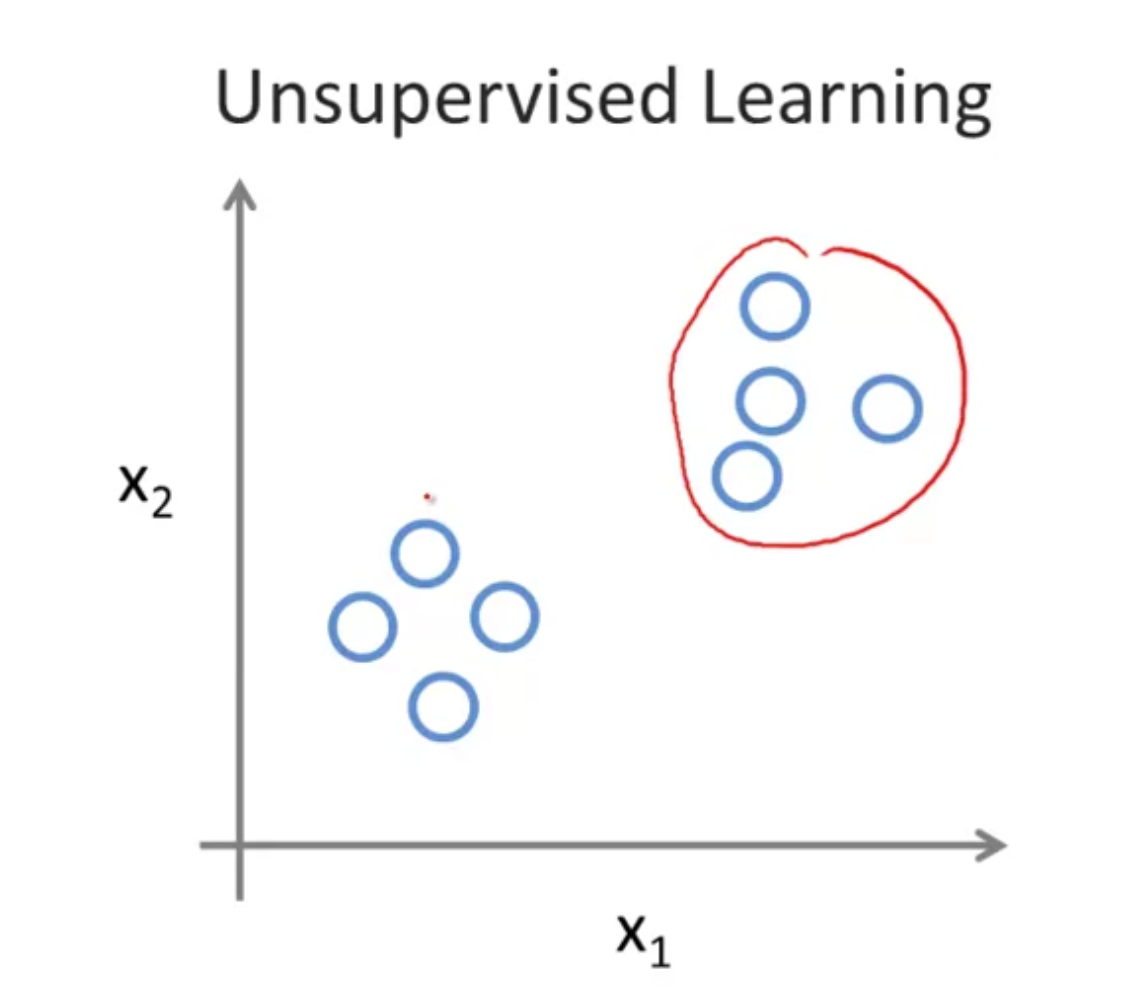
聚类算法被用于新闻推荐,基因辨别,计算机集群组织,市场分类等问题,还有著名的鸡尾酒会问题。
模型表示
$m$ 表示训练集数量
$x$ 表示输入的变量或特征
$y$ 表示输出
$(x, y)$ 表示一个训练样本
$(x^{(i)}, y^{(i)})$ 表示第$i$ 个训练样本
监督学习通过学习算法从训练集中学习一个假设,其流程如图所示。
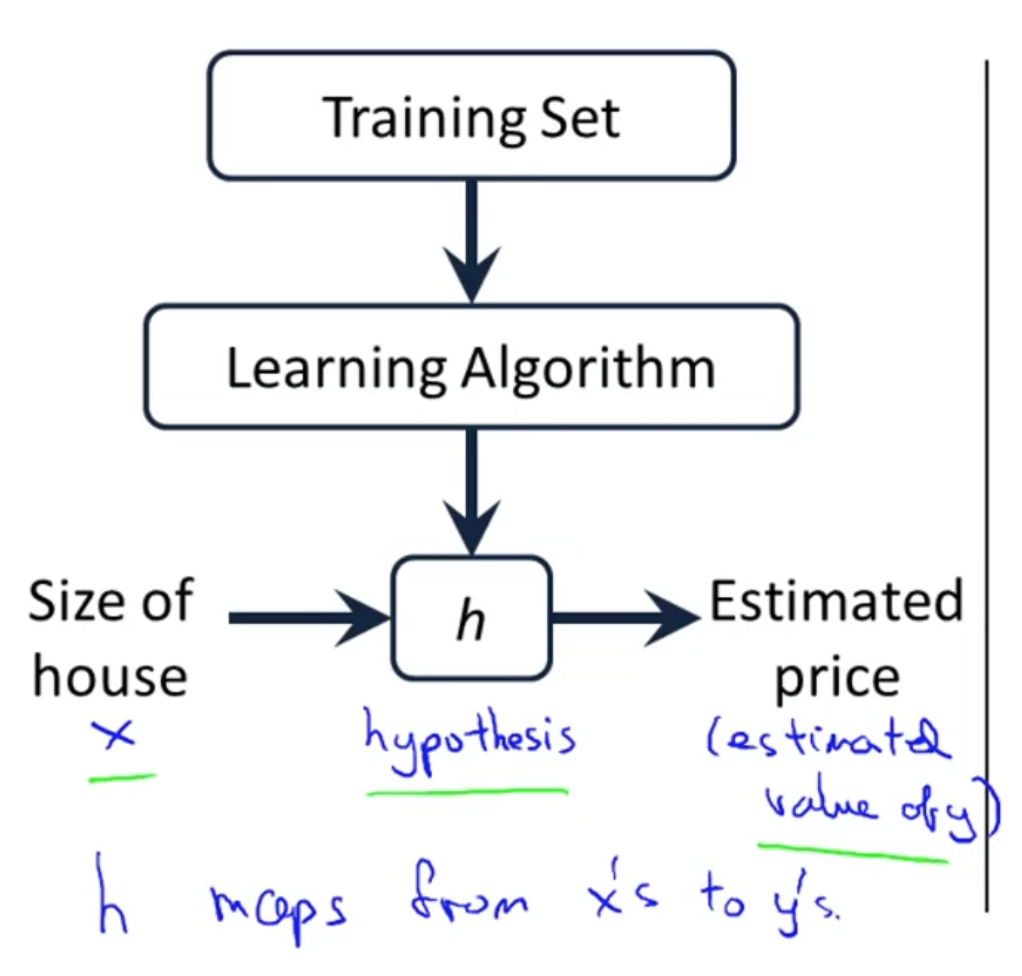
一个简单的监督学习算法称为线性回归,其公式为$h_\theta(x)=\theta_0+\theta_1x$ (单变量线性回归)。
代价函数
以线性回归$h_\theta(x)=\theta_0+\theta_1x$为例。
线性回归优化的目的是对于每个训练样本$(x, y)$,令假设的预测值$h_\theta(x)$尽可能接近标签$y$。
这个问题可以表示为一个最小化问题,即
$$\mathop{minimize}\limits_{\theta_0, \theta_1}\frac{1}{2m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$用$J$表示代价函数,将以上公式改写为
$$J(\theta_0, \theta_1)=\frac{1}{2m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$$$\mathop{minimize}\limits_{\theta_0, \theta_1}J(\theta_0, \theta_1)$$这个代价函数的意义是找到使$J(\theta_0, \theta_1)$最小的$\theta_0, \theta_1$值,上述代价函数也被称为平方差函数,之所以在上面乘一个$\frac{1}{2}$是为了方便计算梯度下降,因为平方的导数项会抵消这个$\frac{1}{2}$。
实际上,假设函数$h_\theta(x)=\theta_0+\theta_1x$是一个关于输入变量$x$的函数,而代价函数$J(\theta_0, \theta_1)=\frac{1}{2m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$
是一个关于假设函数中参数$\theta_0, \theta_1$的函数。
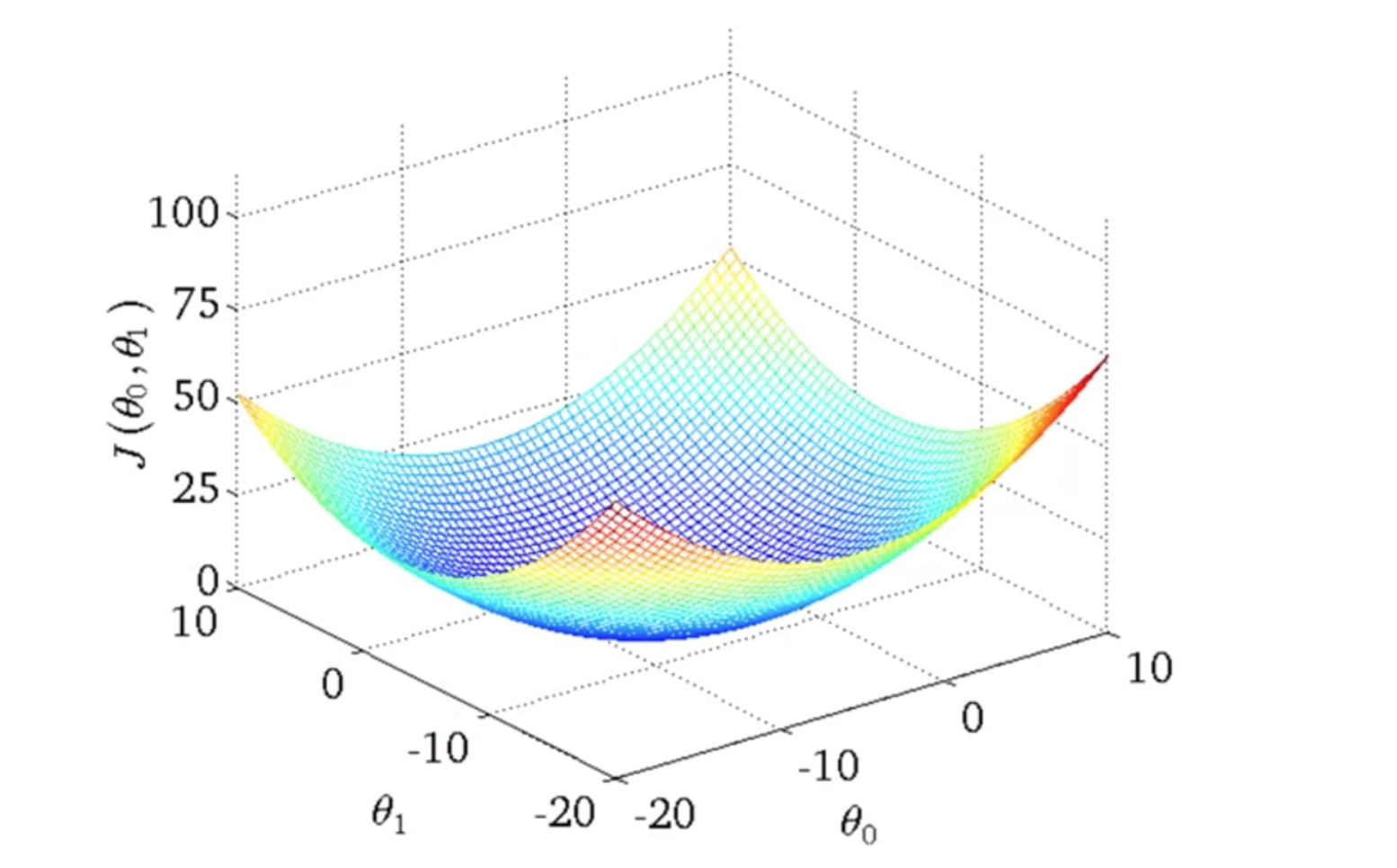
平方差代价函数的图像如下图所示,代价函数的目标是找到一组$\theta_0, \theta_1$值使得代价函数最小化,也就是找到下图中的最低点。