无监督学习

数据通常不带有任何标签

将无标签数据输入到算法，让算法寻找数据隐藏的结构

用途：

市场分割，社交网络分析，聚类算法组织计算机集群，分析银河系构成

K-Means

Step1:随机生成两点作为聚类中心（将数据分几类就生成几点）

Step2:遍历数据集随机将数据分类

Step3:移动聚类中心，计算一个类型所有点的均值，将聚类中心移动到均值处

Step4:根据点距离哪个聚类中心更近，重新分配每个点的类别

repeat Step3 and Step4

代价函数

$J(c^{(1)},\cdots,c^{(m)},\mu_1,\cdots,\mu_K)=\frac{1}{m}\sum\limits_{i=1}^m||x^{(i)}-\mu_{c(i)}||^2$

其中$c^{(i)}$代表当前样本$x^{(i)}$所属的簇的编号，$\mu_k$代表第k个聚类的中心，$\mu_{c(i)}$表示$x_{(i)}$所属簇的聚类中心

这个代价函数的目的就是让所有点到其所属聚类中心的距离最短

实际上可以把K-Meas算法的循环过程分为两个部分，第一部分保持$\mu_i$不变，通过选择$c^{(i)}$最小化代价函数，也就是将每个点分到离他最近的聚类中心的偶成，第二部分保持$c^{(i)}$不变，选择$\mu_i$最小化代价函数，也就是重新计算聚类中心

随机初始化

如何避开局部最优

多次初始化并执行K-Means算法，在所有结果中选择代价函数最小的一个

这种方法对于$K$值较小时效果更好

选取聚类数量

肘部法则：

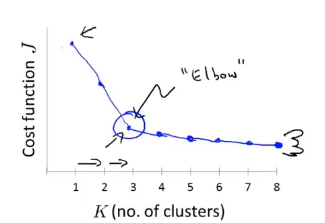
如果代价函数随$K$值变化曲线上有明显的拐点，那么拐点处的$K$值或许就是要选取的聚类数量$K$，如果变化曲线没有明显拐点则肘部法则不适用

更普遍的情况是通过任务的需求来选取聚类数量，例如使用K-Means做多分类，要把数据分为几类就选取多少个聚类